Offline Signature Verification

Source code

Project Overview

This project utilises the EfficientNetV2 as the feature extraction backbone and complemented with a custom loss function inspired from Hard negative examples are hard, but useful, $L_{SC+}$. This project also utilises an extended version of the conventional PK sampling technique, $PKFM$. All of these choices were made to address known limitations and challenges of utilising deep learning models in offline signature verification.

Challenges

• High intra-class variability
• High inter-class similarity
• Poor computational efficiency
• Imbalance of real-world training data

The aim of this model is to maintain intra-class generalisability while maximising distance from skilled forgeries. $L_{SC+}$ reduces the number of active triplets by ignoring easy negatives, yielding comparable or better accuracy with fewer effective gradient updates.

Out of Scope

1. Online signatures
2. Non-Latin languages
3. Accuracy when poor quality images are used
4. Writer dependent verification
5. Signature extraction

Like all models placed in critical systems, they can sometimes make potentially disastrous mistakes and require human oversight.

Problems

To the best of my knowledge, albeit a bit questionable, most offline signature verification systems are still largely manual.

I was informed of this during my internship

Unlike machines, humans cannot operate on high volumes at high speed over a long continuous period of time. Since signatures are still used in important documents, particularly in financial, legal, and administrative contexts, errors are very often unacceptable.

Deep learning approaches also often struggle with intra-class variability and skilled forgeries. So, a lot of approaches cheat by implementing machine learning models on top. There is nothing wrong with this approach, but I refuse to think that we have reached the limits of deep learning models in OSV. This isn’t just an issue with the architecture of the models, but rather the inherent private nature of signatures, leading to a lack of real-world signatures.

If developers aren’t careful enough, OSV models that utilise the triplet loss approach can suffer from poor optimisation, wasting resources. Most of the time, positives are much closer to the anchors than the negatives, leading to over-optimisation of anchor-positive and cause overfitting.

Read about triplet loss here

Approach

Pre-Processing Images

Since what we want from the signature images are the strokes, colours do not play much of a role. RGB format would have irrelevant colour information which may interfere with the model’s ability to effective extract the relevant feature embeddings. In contrast, grayscale or black and white forces the model to focus solely on intensity differences by enhancing the contrast between the strokes and the background. All in all, grayscale/BW essentially reduces noise and improves the model’s ability to identify key patterns.

Although greyscale images reduces unnecessary information, it sometimes makes the strokes less discernible from the background; this impacts the model’s feature extraction ability. To make the strokes pop out, I went with Otsu’s thresholding which automatically determines the optimal global threshold needed to convert the grayscale image into a binary image.

For example,

Before	After

Now, there is a clearer distinction of the strokes from the background, reducing noise.

Unfortunately, I can’t solve the lack of data issue that plagues this challenge and most signature datasets require me to sign an agreement, so I opted for the CEDAR dataset and applied data augmentation; I applied resizing, rotation, scaling, and translation to artificially boost the number of training samples.

Example 1	Example 2

Backbone

Training a CNN model that is accurate from scratch would require tens of thousands to millions of examples to reach high accuracy. Fortunately, I can utilise transfer-learning to speed up the process while ensuring accuracy.

Picking a backbone wasn’t difficult, PyTorch already offers pretrained CNN models and… it’s a lot of models.

- AlexNet
- ConvNeXt
- DenseNet
- EfficientNet
- EfficientNetV2
- GoogLeNet
- Inception V3
- MaxVit
- MNASNet
- MobileNet V2
- MobileNet V3
- RegNet
- ResNet
- ResNeXt
- ShuffleNet V2
- SqueezeNet
- SwinTransformer
- VGG
- VisionTransformer
- Wide ResNet

After doing some homework and this book, EfficientNetV2 became my pick. The model fixes everything wrong with EfficientNetV1, balancing width, depth, and resolution. The model performs $11\times$ faster and $6.8\times$ smaller while achieving high accuracy. Amongst the 3 available EfficientNetV2 variants, the mid-size variant offers a strong balance between computational cost and performance. The largest variant contains more than twice the parameters of M, yet it yielded only marginal performance on ImageNet.

Models	Top-1 Accuracy (%)	Parameters
EfficientNetV2-S	83.9	22M
EfficientNetV2-M	85.1	54M
EfficientNetV2-L	85.7	120M

Check out the full results here: EfficientNetV2: Smaller Models and Faster Training

I removed the classification head and replaced it with project layers that reduce the feature vectors to 256 dimensions.

Why 256?

Short answer:

It’s a nice middle ground

Long answer:

256 dimensions provide a rich yet efficient feature space for encoding patterns. Since signature images are relatively simple there is no need for a higher level of dimensions as a higher dimension can lead to redundancy.

Loss Function

Triplet Loss

A conventional loss function functions as follows:

There are three nodes, collectively called triplet, comprising an anchor, a genuine signature (positive), and a forged signature or a signature from a different signer (negative). The goal is to pull similar images (anchor and positive) closer together while pushing dissimilar images (anchor and negative) farther apart. This is achieved by ensuring that the anchor is closer to the positive than to the negative by at least margin $\alpha$.

$$\begin{array}{r}{D}_{ap}+\alpha <D_{an}\end{array}$$

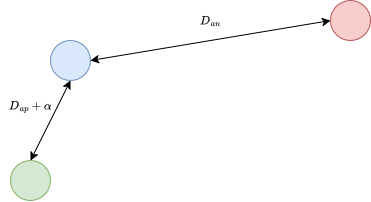
However, many triplets generated may already satisfy this constraint, resulting to slow convergence if these triplets are still passed through the network. To address this, the authors of this paper, introduced online triplet mining to dynamically compute the triplets as training progresses. Online mining is achieved by constructing large mini-batches that contain multiple examples per identity, selecting anchor-positive pairs from within the batch, and then dynamically identifying negatives.

• For hard triplets, the negative is chosen as the closest impostor to the anchor.
• For semi-hard triplets, the negative is farther than the positive but still lies within the margin.

Hard Triplet	Semi Hard Triplet

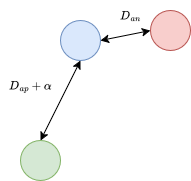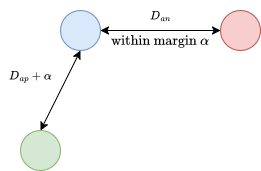This paper is particularly important as it shows that this loss function is ideal for verification problems involving negative samples. Their online mining approach also led to countless inspirations down the line.

I decided to implement this loss function to make a comparison with the loss function that I will be making.

$L_{SC}+$

This loss function is an extension of Hard negative examples are hard, but useful.

The authors of Hard negative examples are hard, but useful noticed that the conventional triplet loss function has a couple of issues: poor optimisation and gradient entanglement. To address this, they proposed to simply ignore anchor-positive pairs and easy negatives to focus solely on penalising hard negatives.

This approach works well in the domain of offline signature verification; the high intra-class variation requires the model to have some generalisability and the presence of skilled forgeries needs a robust model. The combination of these two characteristics is what makes this problem so challenging.

However, there is a subtle failure that may happen. By removing explicit constraints on anchor-positive similarity, the model is no longer encouraged to keep genuine signatures close together. Over time, genuine embeddings can drift apart.

In practice, this can lead to false negatives: a genuine signature sampled later may fall outside of the verification threshold, even though it belongs to the same user.

To mitigate this, I introduced a lightweight positive constraint that softly enforces intra-class cohesion while retaining the hard-negative emphasis. This lets me utilise the benefits of the existing loss function while preventing genuine signatures from drifting too far apart.

$$\begin{array}{r}{L}_{SC+}=L_{SC}(S_{ap},S_{an})+\mu L_{\text{pull}}\end{array}$$

Where:

• $L_{SC}$ is Selectively Contrastive Triplet Loss
• $L_{\text{pull}}$ is Positive Pull Regularisation
• $\mu$ is a hyperparameter weighing the positive pull

The $L_{SC}$ handles the inter-class separation, whereby it switches behaviour according to the difficulty of anchor-negative pairs (source).

$$\begin{array}{r}{L}_{SC}\left(S_{ap},S_{an}\right)=\{\begin{array}{r}\lambda S_{an}\\ L\left(S_{ap},S_{an}\right)\end{array}\begin{array}{c}if{S}_{an}>S_{ap}\\ otherwise\end{array}\end{array}$$

Where:

• $S_{ap}=f_a^T{f}_p$ is cosine similarity between anchor and positive
• $S_{an}=f_a^T{F}_n$ is cosine similarity between anchor and negative
• $\lambda$ is weighting factor for hard negatives

This is more computationally efficient compared to the standard triplet loss implementation. If a negative sample is found to be closer to the anchor than the positive sample (a hard negative), the loss function switches and pushes the negative sample away from the anchor in the hypersphere; the negative sample will receive exponentially larger weighting in the loss function. In contrast, when a negative sample is already sufficiently distant (an easy negative), the model does not incur any penalty and simply ignores it by switching to smooth, self-normalising log-softmax, receiving vanishingly small weights.

The $L_{\text{pull}}$ is defined as follows:

$$\begin{array}{r}{L}_{\text{pull}}=\{\begin{array}{r}m-S_{ap},\\ 0,\end{array}\begin{array}{c}if{S}_{ap}<m\\ \text{otherwise}\end{array}\end{array}$$

Where:

• $m$ is margin

The margin is important to stop the model from over-optimising positives. If a margin is not included, the model may ignore its initial purpose to maximise negative distances. This subsequently leads to the collapse of the embedding space. Once the anchor-positive similarity exceeds the threshold, the gradient from the positive pull becomes 0, allowing the model to focus on separating negatives.

Dataset and Sampling

The dataset is split based-on signer identity rather than individual images, ensuring that no signature from a given signer appears in both training and testing sets. This prevents leakage of testing image into training and enforces subject-independent evaluation.

In standard $PK$ sampling, a batch is formed by selecting $P$ signers and $K$ signatures per signer, controlling the balance between inter-class and intra-class samples. However, it lacks the control over hard negatives and easy negatives.

My approach to this is to create a signature mapping that associates each signer with their signatures (both original and forgeries). Instead of loading the images upfront, I store the paths to the images and defer rendering until training. This optimises memory usage and reduce unnecessary overhead. $PKFM$ introduces two additional parameters, $F$ and $M$, which regulates the number of intra-class and inter-class negatives, respectively. Increasing $F$ raises the likelihood of encountering hard negatives (skilled forgeries), while increasing $M$ introduces more easy negatives (inter-class negatives), thereby enriching the diversity of each batch.

The resulting batch size is:

$$\begin{array}{r}\text{Batch Size}=P\times (K+F+M)\end{array}$$

From a practical standpoint, offline signature datasets are often imbalanced, with some signers contributing disproportionately more samples. If not handled with care, some signers experience stronger verification compared to signers with fewer signatures. $PKFM$ mitigates this issue by balancing the dataset at the batch level.

Training

I implemented key features for training such as:

• Early Stopping
  • Monitors validation loss and automatically halts training if no significant improvement is observed over a set number of epochs, preventing overfitting
• Learning Rate Scheduling
  • Manages the adjustment of the learning rate throughout training to optimise convergence.
• Checkpointing
  • Automatically saves model snapshots - weights, and optimizer state - at key points when a new best validation loss is achieved, ensuring progress can be restored and the best model recovered.
• Device Management:
  • Handles moving data and the model to the GPU for accelerated computation.

To ensure a fair comparison of all the models, same configurations for the model, scheduler, optimiser, and training are used. The margin hyperparameter is also fixed at 0.5 across all loss functions, ensuring that the differences in performance are attributable to the loss formulation rather than margin selection. The hyperparameters values are also selected based on the recommended starting points. (Can’t afford an extensive hyperparameter fine tuning at the moment)

For my run, I implemented a linear warm-up for the first 5 epochs, gradually increasing the learning rate from 0.0001 to 0.001, followed by a cosine decay learning rate schedule that smoothly reduces the rate to $1\times 10^{-6}$. This method stabilises early training and enables fine-grained convergence .

Results

Hard Triplet Mining

Under batch hard mining, the model managed to separate negative samples from the positive samples relatively well; at the start of training, the mean of attraction term was higher compared to the mean of repulsion term.

Attraction Term	Repulsion Term

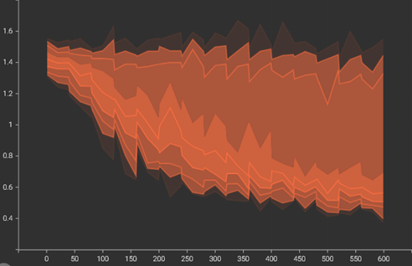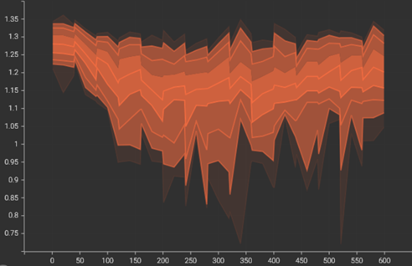The histograms also show desired changes as the area of concentration for repulsion term stayed on the right while the area of concentration of attraction term shifted to the left.

Attraction Term	Repulsion Term

When tested on the test set, the model reported acceptable results: the model achieved an overall classification accuracy of 78.23%. In other words, the system correctly identified the signatures in approximately 78 out of every 100 cases, demonstrating acceptable performance within the context of the evaluation. The relatively high anchor-positive cosine similarity score (positive score) and the low anchor-negative cosine similarity score (negative score) indicates that the model can discern the forgeries from the original signatures. Moreover, across all the thresholds, with the best threshold, 0.667, misclassification happens $21.77\%$ of the time.

Category	Metric / Score	Result
Performance	Accuracy	78.23%
	True Positive Rate	78.20%
	False Positive Rate	21.80%
	AUC	0.8607
	EER	21.77%
Similarity Score	Positive Score	0.7784
	Negative Score	0.3611

The smooth ROC curve with an AUC of 0.8607 indicates an embedding space that retains a fair amount of class separability across varying decision thresholds.

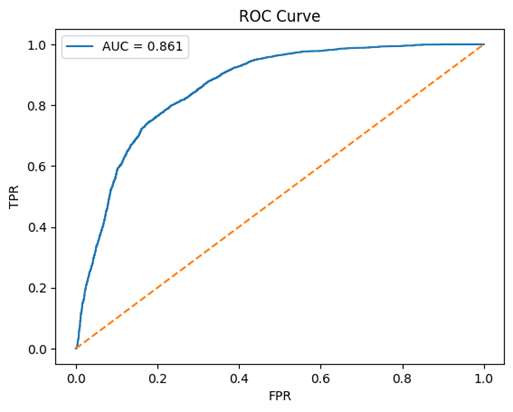
But, the high false acceptance rate is still a concern. This demonstrates that while hard-negative mining successfully increases inter-class separation for the hardest violations, it does not guarantee robust generalisation against all forgery types, especially those that are less extreme or unseen during training.

Semi Hard Triplet Mining

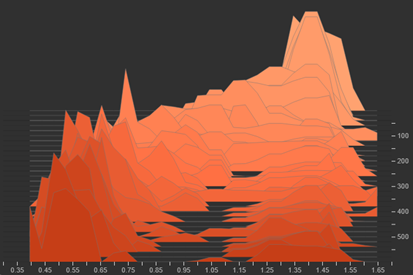
Under batch hard semi mining, the model also managed to separate negative samples from the positive samples relatively well; at the start of training, the mean of attraction term was similar to the mean of repulsion term; at the end of training, the mean of repulsion term were mostly concentrated between 1.1 and 1.2, while the mean of attraction term lowered from around 1.4 to around 0.7.

Attraction Term	Repulsion Term

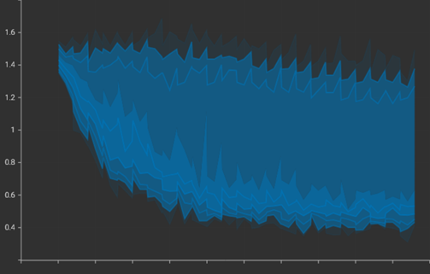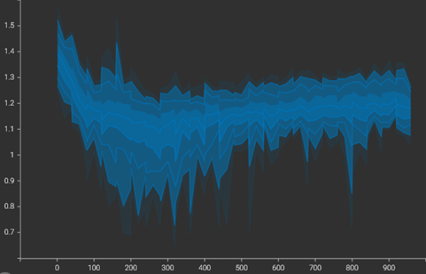The histograms also showed desired changes as the area of concentration for repulsion term stayed on the right while the area of concentration of attraction term shifted to the left. Although, the histogram for repulsion term looks as though it shifted to the centre instead of the right, this is due to the high distance recorded at the start of the training, misleading interpretation. The shifting histograms suggest that the model is learning consistent boundaries rather than overfitting to a few extreme cases.

Attraction Term	Repulsion Term

When tested on the test set, the model has a high recall rate of 82.10% and a false positive rate of 17.90%, meaning the model can correctly discern the forgeries from the original signatures most of the time. Additionally, the model reported high positive score and mid-range negative score, denoting the model’s ability to cluster positives while some-what separating negatives. Finally, with a threshold in which the model performs best on, 0.777, the model yields an error rate of 17.88%.

Category	Metric / Score	Result
Performance	Accuracy	82.12%
	True Positive Rate	82.10%
	False Positive Rate	17.90%
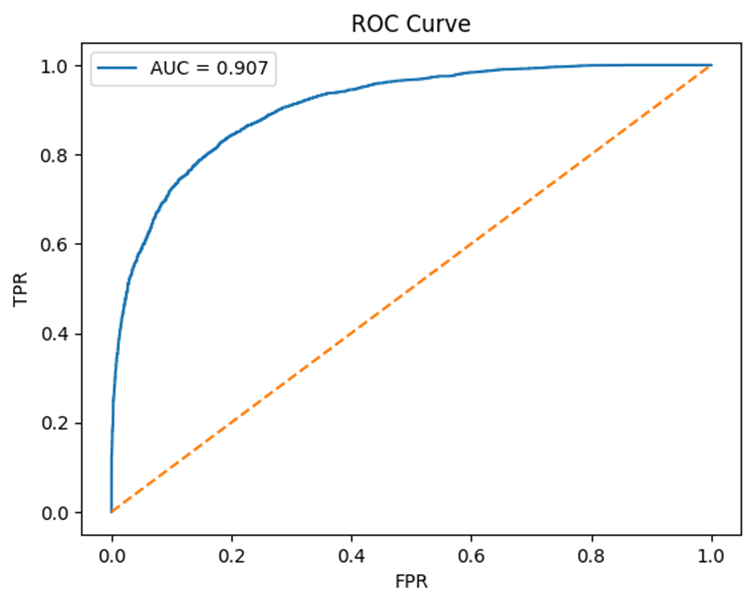
	AUC	0.9071
	EER	17.88%
Similarity Score	Positive Score	0.8639
	Negative Score	0.4967

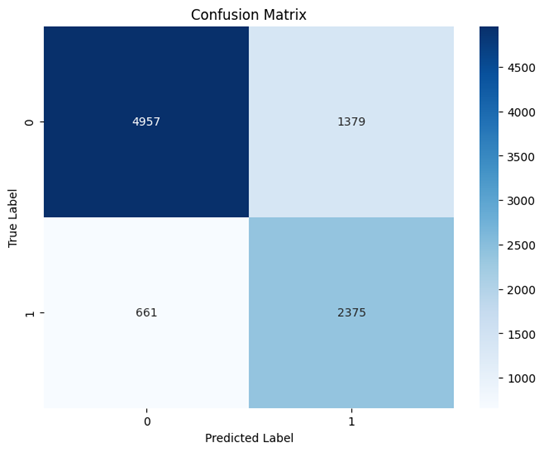
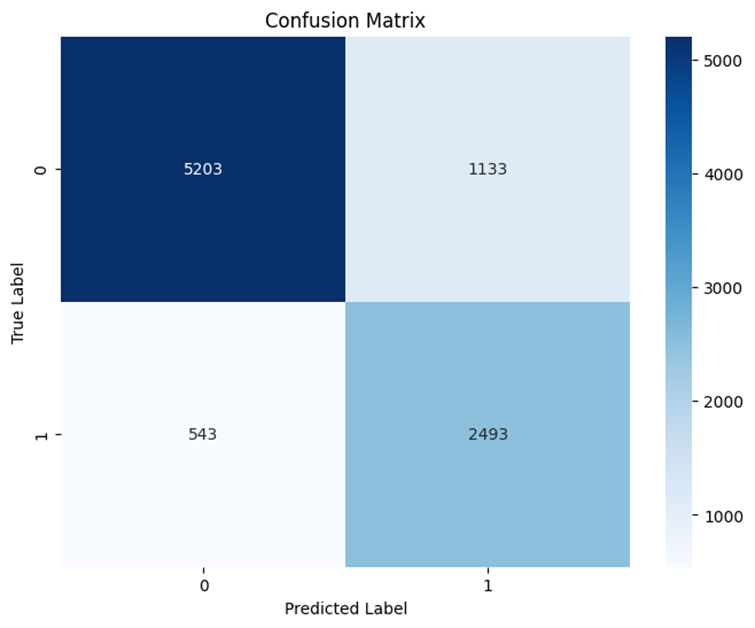
Semi hard mining produced smooth and more globally consistent boundaries, as observed by the cleaner ROC curve. Although the confusion matrix still shows some leakage of difficult forgeries, the overall pattern suggests that semi-hard mining produces a balanced embedding space with dependable separation without being overly sensitive to difficult negatives.

ROC Curve	Confusion Matrix

$L_{SC+}$

Unlike triplet loss, the $L_{SC+}$ loss function flips the positive and negative intuition. The process of pushing hard negatives away is implemented with cosine similarity, where the lower the value, the more dissimilar the points are. On the other hand, the addition of a positive pull causes the attraction term to increase, but only up to the margin provided.

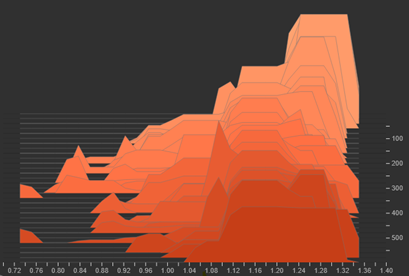
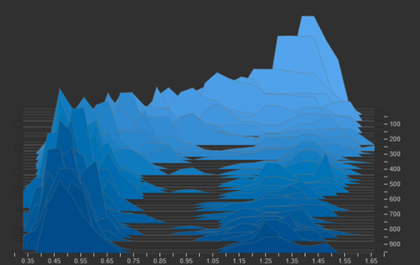
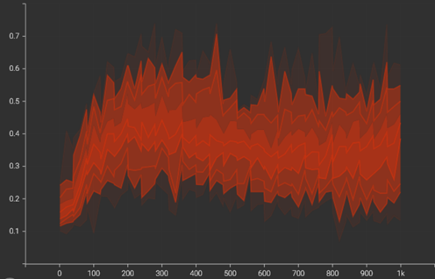
The model recorded the expected behaviour during training – rising attraction term and reducing repulsion term.

Attraction Term	Repulsion Term

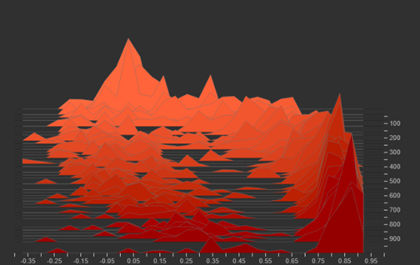
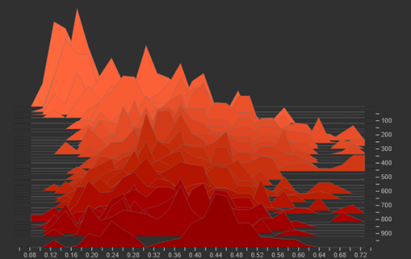
The histograms of repulsion term are spread out, showing areas of concentration for both easy and hard negatives. The distribution of repulsion values indicates that the model is handling both easy and difficult negatives rather than collapsing around a narrow boundary.

Attraction Term	Repulsion Term

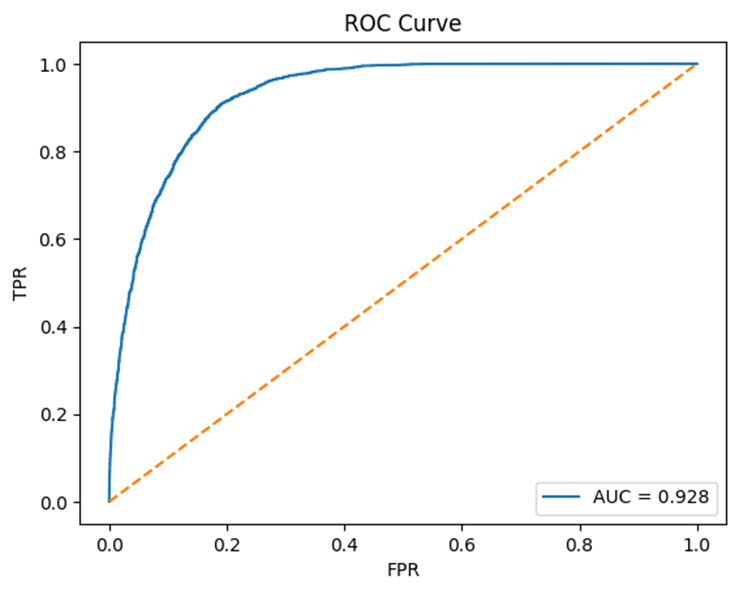
The model reported promising results on the test set; it scored 84.80% on the recall rate, 15.20% on false positive rates, and an accuracy of 84.85%. The high positive score and low negative score denote the model’s capability to separate signatures. Moreover, at threshold 0.725, a respectable equal error rate of 15.15% was recorded.

Category	Metric / Score	Result
Performance	Accuracy	84.85%
	True Positive Rate	84.80%
	False Positive Rate	15.20%
	AUC	0.9284
	EER	15.15%
Similarity Score	Positive Score	0.8444
	Negative Score	0.3644

The higher recall, lower false-positive rate, and stronger AUC point to a cleaner, more discriminative embedding space than the triplet-based variants. Although some errors remain, the overall implication that $L_{SC+}$ yields the most robust separation of signatures among the test configurations, with better generalisation and a more stable boundary.

ROC Curve	Confusion Matrix

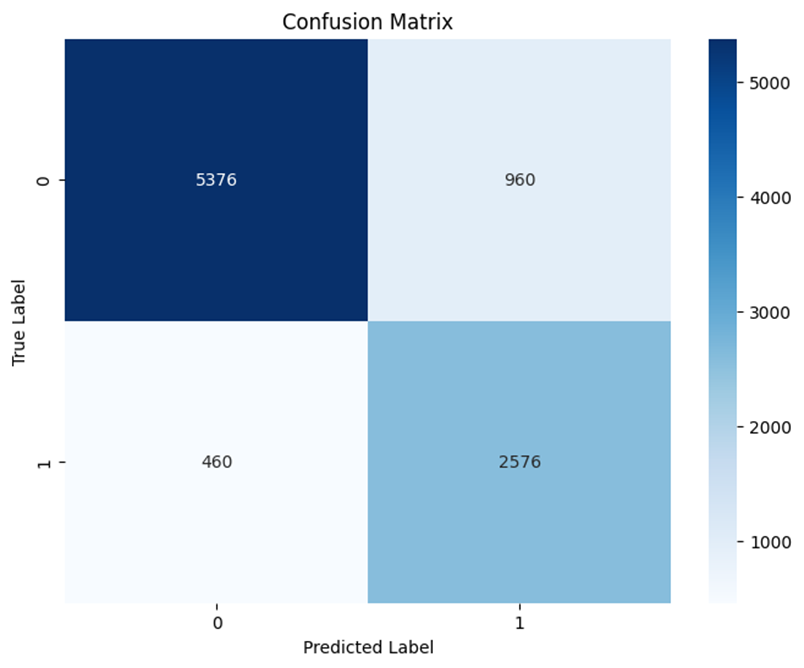Discussion

These results reflect models trained without extensive hyperparameter fine-tuning. Across all loss functions, the models exhibit the desired behaviour: a leftward shift of anchor-positive distance and a lingering anchor-negative distance on the right.

However, upon scrutiny, some nuances can be observed; there exist overlapping between the attraction and repulsion terms. The extent of this overlap and resulting stability varies significantly by strategy.

Hard triplet mining shows the most severe overlap between positive and negative distributions. This results in a higher rate of false predictions, even at the model’s optimal performance threshold. This aligns with the observation made by the authors of FaceNet, who noted that an over-focus on hard triplets often causes model collapse. The excessive penalty on hard negatives forces the model to over-compress anchor-positive pairs to compensate. This over-fitting to specific hard samples reduces generalisation to unseen signatures from the same signer. The imbalance focus on hard negatives results in inconsistent separation of anchor-negative pairs, leaving some negatives closer to the anchor than desired.

Semi hard triplet mining exhibits less drastic overlap. This is likely due to its enforcement of separations based on $D_{ap}+\alpha$ rather than purely focusing on the hardest violations. However, this strategy can backfire when the threshold for forgeries falls within the $D_{ap}+\alpha$ range, where false predictions remain relatively high. Notably, its reduced emphasis on hard triplets leads to slightly more dispersed anchor-positive pairs, increasing robustness to intra-class variation by allowing natural differences in genuine signatures.

Amongst the three loss functions, $L_{SC+}$ performs the best. While some overlap persists, it is minimised compared to the other strategies. This is likely due to its trait of ignoring easy negatives, leading to closer, yet acceptable, distances. At the optimal threshold, this model yields the lowest false acceptance of forgeries.

$L_{SC+}$ scored the highest in TPR, AUC, and accuracy.

Metric / Score	$L_{SC+}$ (0.725)	Semi-Hard Triplets (0.777)	Hard Triplet (0.667)
TPR	84.8%	82.1%	78.20%
FPR	15.2%	17.9%	21.80%
AUC	0.9284	0.9071	0.8607
Positive Score	0.8444	0.8639	0.7784
Negative Score	0.3644	0.4967	0.3611

It is observed that both the positive and negative scores of $L_{SC+}$ fall between those of semi hard (0.8639) and hard mining (0.7784). While this may seem counterintuitive, this highlights a critical point: a higher positive similarity does not necessarily translate to better verification. What matters is the margin between positive and negative distributions. $L_{SC+}$ achieves this by moderately enforcing intra-class compactness while consistently pushing hard negatives, creating more balanced clusters.

The ability to decouple anchor-positive and anchor-negative distances allows $L_{SC+}$ to receive independent gradient signals, ensuring continuous, informative updates regardless of triplet sampling quality. In contrast, the coupling effect in hard and semi- hard triplet mining causes imbalance gradients, leading to overlap. The smoother gradient dynamics of $L_{SC+}$ result in a more separable embedding space, improving discriminability across thresholds (higher AUC and lower EER).

The operating threshold for $L_{SC+}$ falls between semi-hard and hard mining, reflecting a more balanced embedding distribution. By comparison, the lower threshold required by hard triplet ming reflects its tendency to over-compress positives, which shifts the negative distribution closer and increases false acceptance of forgeries.

Overall, the results indicate that $L_{SC+}$ produces more stable, generalizable, and discriminative embeddings. Despite not achieving the highest raw positive score, its improved separation of positive and negative distributions leads to superior AUC, TPR, FPR, and accuracy. This robustness arises from its decoupling of anchor-positive and anchor-negative contributions, which ensures continuous informative gradients and balanced embedding clusters.

Conclusion

This project has developed a signature verification model that addresses key limitations in conventional verification systems. By introducing $L_{SC+}$ loss function and integrating it with the state-of-the-art vision EfficientNetV2 backbone, the model achieves robust performance in distinguishing genuine signatures from forgeries, as demonstrated by consistently superior evaluation metrics.

In addition, the project extends $PK$ sampling to $PKFM$ sampling strategy, which is applicable to verification problems involving both positive and negative samples. The decoupling approach of $L_{SC+}$ provides a principled and intuitive mechanism for separating anchor-positive and anchor-negative samples, reducing training variance and improving generalisation compared to traditional mining strategies. Even without extensive hyperparameter fine-tuning and limited data, $L_{SC+}$ consistently outperforms semi-hard and hard triplet mining, proving its effectiveness in offline signature verification.

Overall, this work demonstrates strong potential for real-world application in biometrics verification. The proposed contributions not only advance signature verification research but also offers a scalable framework that can be extended to other biometric modalities, making it a valuable addition to the broader field of biometric security.

Implementation and Deployment

Future implementation

Previous version

I developed a backend API using Flask to handle verification requests.

A simple frontend is developed with React and a backend is developed using Flask microweb framework. I decided to implement a vector database using PostgreSQL with an open source plugin, pgvector. Finally, the entire system was containerised using Dockerfor easy deployment and testing.

The webpage allows the user to insert a signature image along with the user’s details, and upon verification, the similarity score, confidence score, Euclidean distance, and the distance score will be calculated and displayed.

Future Developments

1. Extensive hyperparameter fine-tuning
2. Implementation and deployment
3. Try different datasets
4. Ironing-out more kinks

References

I have to give credit where credit is due

1. EfficientNetV2
2. Hard negative examples are hard, but useful
3. FaceNet: A unified embedding for face recognition and clustering
4. Otsu’s Method
5. CEDAR